Definição

Os números complexos ganharam importância no final do século XVII e início do século XIX quando a ideia surgiu a ideia de associar o ponto P(a,b) do plano cartesiano xOy ao número complexo z = a + bi, onde se convencionou associar os pontos xO e yO, a parte real e imaginária, respectivamente.

Dessa forma, a cada número complexo z = a + bi corresponde um ÚNICO ponto P (a, b) do plano.

O ponto P é chamado afixo ou imagem geométrica de z.

O plano cartesiano é chamado plano complexo ou  plano de Argand-Gauss. O eixo Ox é o eixo real, e o Oy, eixo imaginário.

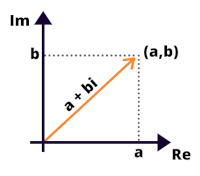
Vamos ver alguns exemplos:

1 - Vamos determinar a imagem geométrica dos números complexos: z₁ = 3 + 2i, z₂ = -1 + i, z₃ = 3 - 2i, z₄ = 2 e z₅ = 3i.

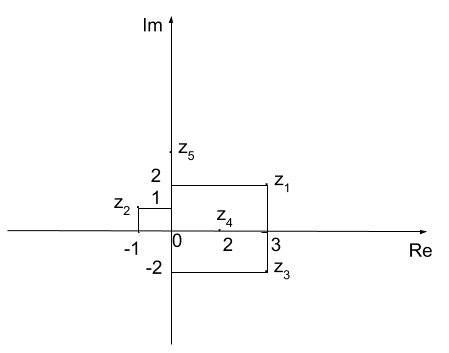
z1, associa os pontos P1 (3, 2)

z2, associa os pontos P2 (-1, 1)

z3, associa os pontos P3 (3, -2)

z4, associa os pontos P4 (2, 0)

z5, associa os pontos P5 (0, 3)

Os pontos P4 e P5 representam, respectivamente, um número real e um imaginário puro. Daí, nota-se, de P4, que todo número real tem imagem sobre o eixo Re e que todo número imaginário puro, P5, tem imagem sobre o eixo Im.

Agora é a sua vez

1 - Determine, no plano de Argand-Gauss, o afixo e cada um dos seguintes números complexos:

a) z₁ = 1 + 3i

b) z₂ = -2 + 3i

c) z₃ = -1 + 5i

d) z₄ = -2 - 3i

e) z₅ = -4 + 2i

f) z₆ = 4 - i

2 - No plano de Argand-Gauss, as imagens de z₁, z₂ e z₃ são, respectivamente, (3, 2), (4, -1) e (-3, 0).

a) Escreva z₁, z₂ e z₃ na forma algébrica?

b) Qual a imagem do complexo  z₁ - 2.z₂ + z₃?

Módulo

Chama-se módulo de um número complexo, z = a + bi, o número real não negativo $\left|z\right| = \sqrt{a^2 + b^2}$.

(O módulo de z é comumente representado pela letra grega 𝞺: lê-se: ‘rô’).

Geometricamente, calcular o módulo de z é equivalente a calcular a distância entre a origem e o ponto Z (dOZ), como no gráfico abaixo.

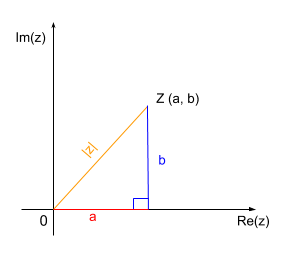
Vamos ver alguns exemplos:

1 - Calcule o módulo dos números complexos, abaixo:

a)  z = 1 + i

Solução: $z = \sqrt{1^2 + 1^2} = \sqrt{2}$

b) z  = -2i

Solução: Como z é um imaginário puro, então, Re(z) = 0. Portanto,

 $$\begin{gathered} \left|z\right| = \sqrt{0^2 + {(-2)}^2} \\ \left|z\right| = \sqrt{4} = 2 \end{gathered}$$ 

c) z = 3

Solução: Como z é um número real, então, Im(z) = 0. Portanto, 

$$\begin{gathered} \left|z\right| = \sqrt{3^2 + 0^2} \\ \left|z\right| = \sqrt{9} = 3 \end{gathered}$$

d) z  = -i

Solução: Como, a = 0 e  b = -1, então, z é um número imaginário puro, basta mudar o sinal de b (pois, b é negativo). Logo, |z| = 1. 

e) $z = \sqrt{10}$.

Solução:  Como, a = 10 e  b = 0, então, z é um número real, basta manter o sinal de a (pois, a é positivo). Logo, $\left|z\right| = \sqrt{10}$. 

f) $$\begin{gathered} \left|z\right| =\sqrt{ {\left(3\right)}^2 + {(-1)}^2} \\ \left|z\right| =\sqrt{3 + 1} = \sqrt{4} \\ \left|z\right| =2 \end{gathered}$$

2 - O módulo do número complexo z = x + 3i é 5. Determine x.

Solução: 

$\left|z\right| = \sqrt{a^2 + b^2}$

$5 = \sqrt{x^2 + 9} \iff 5^2 = {(\sqrt{x^2 + 9} )}^2$

$5^2 = x^2 + 9 \iff 25 = x^2 + 9$

$25 - 9 = x^2 \iff 16 = x^2$

$x = \sqrt{16} \iff x = \pm 4$

Agora é sua vez

1 - Calcule o módulo dos seguintes números complexos

a) z = -1 + i. Resposta: 2.

b) z = 8 - 6i. Resposta: 10.

c) z = -6i. Resposta: 6.

d) z = -8. Resposta: 8.

e) $z = \frac{2 - 3i}{1- i}$.  Resposta: $\frac{\sqrt{26}}{2}$.