O grupo tem 20 pessoas:

a + b + c + x + y + z + 3 = 20

a + b + c + x + y + z = 17  (I) 

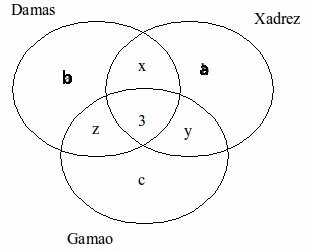
Xadrez tem 12:

a + x + y + 3 = 12

a + x + y = 9 (II)

Damas tem 15:

b + x + z + 3 = 15

b + x + z = 12 (III)

Gamão tem 6:

c + y + z + 3 = 6

c + y + z = 3 (IV)

Somando II + III + IV:

a + b + c + x + y + z + x + y + z = 24 (V)

Usando I em V

(a + b + c + x + y + z) + x + y + z = 24 

17 + x + y + z = 24

x + y + z = 7 (VI)

I.Dez pessoas jogam mais de uma modalidade (verdade)

x + y + z + 3 = 7 + 3 = 10 (observe que x + y + z + 3 corresponde as pessoas que jogam mais de uma modalidade)

II. Todas as pessoas que jogam xadrez também jogam damas (falso)

Para isso ocorrer, x + 3 tem que ser 12, isto é, x = 9. 

x não pode ser 9, pois sabe-se que x + y + z = 7.

III. Se, das pessoas que jogam damas, oito jogam xadrez, então uma única pessoa joga apenas gamão (verdade)

Das pessoas que jogam damas, as que jogam xadrez é (x + 3).

Fazendo x + 3 = 8, temos x = 5.

Usando (VI),

x + y + z = 7 

5 + y + z = 7

y + z = 2

Mas em (IV)

c + y + z = 3             (como y + z = 2)

c + 2 = 3 

c = 1

Isto é, uma única pessoa joga apenas gamão.

GABARITO: C