41 - Um levantamento efetuado numa empresa, para verificar quantos funcionários falam inglês ou espanhol, mostrou-se que 30% dos funcionários não falam nenhuma das duas línguas; o número de funcionários que falam apenas inglês é igual ao número de funcionários que falam as duas línguas e o número de funcionários que falam apenas espanhol é 3/2 do número de funcionários que falam apenas inglês.
A porcentagem do número de funcionários que falam inglês é igual a
A) 20%
B) 30%
C) 40%
D) 50%
E) 60%
Solução: Vamos analisar o enunciado:
I: Funcionáriso que só falam APENAS ingles é igual aos que falam as duas linguas, vamos chamar de: x;
II: Os funcionários que falam APENAS espanhol é 3/2 do número de funcionários que falam apenas inglês, então: 3x/2;
III: Funcionários que não falam NENHUMA das linguas: 30%, portanto, 70% dos funcionários falam algumas das línguas;
Fazendo a união dos conjuntos: Apenas Inglês + Inglês e Espanhol + Apenas Espanhol
x + x + 3x = 70
2x + 3x/2 = 70
Reduzindo ao mesmo denominador:
4x + 3x = 140
7x = 140
x = 140/7
x = 20
Logo, x = 20%. Como os que falam inglês é igual a 20%, mas os que falam inglês e espanhol = 20% também, portanto, os funcionários que falam inglês é igual a 40% (perceba que os que falam inglês e espanhol também falam inglês), então, a resposta correta é letra C
42 - Dados os conjuntos M = {x∈N*, m.d.c(x,10)=5} e T = {x∈N*, x≤50}, pode-se afirmar:
A) M - T possui algum elemento que é par.
B) T - M é um conjunto de 45 elementos
C) M possui algum elemento que não é um múltiplo de 5.
D) Nenhum elemento de T - M é múltiplo de 5.
E) M - T é um conjunto de 50 elementos.
Solução: M = {5,15,25,35,45,55,65,75,85,95} e T = {1,2,3,..., 48,49,50}
T - M = {5,15,25,35,45,55,65,75,85,95} - {1,2,3,..., 48,49,50} = {1,2,3,4,6,7,8,9,10,11,12,13,14,16,17,18,19,20,21,22,23,24,26,27,28,29,30,31,32,33,34,36,37,38,39,40,41,42,43,44,46,47,48,49,50}
Logo, T - M possuí 45 elemento, portanto aresposta correta é letra B
43 - Dos conjutos relacionados, o único conjunto vazio é
A) {x∈Q, (√2)x ∈Q}
B) {x∈N, x - √2 ≤0}
C) {x∈N, x - √2≥0}
D) {x∈Q, √2 + x ∈Q}
E) {x∈R - Q, √2 + x ∈Q}
Solução:
A) (√2) x; Existe, pelo menos, um x que perteça a Q;
B) x - √2 ≤0; Existe, pelo menos, um x que pertença N;
C) x - √2≥0; Existe, pelo menos, um x que pertença N;
D) √2 + x ; Não existe um x que solucione a senteça (conjunto vazio);
E) √2 + x; Existe, pelo menos, um x que pertença N;
Logo, a resposta correta é letra D.
44 - O conjunto S = {x∈R, [(x2 - 3)/x] < 2} é tal que:
A) S ⊂ ]-∞, 3[
B) [-1, 3] ⊂ S
C) S ⊂ [-1, 3]
D) S ⊂ [3, +∞]
E) [-∞, 0] ⊂ S
Solução:
[(x2 - 3)/x] < 2 => x2 - 3 < 2x => x2 - 2x - 3 < 0
Δ = 16 e x’ = 3 e x’’ = -1
S = {x∈R/-1
Logo, S = ]-1, 3[, portanto, a resposta correta é letra A.
45 - Os números complexos z1 e z2 possuem afixos que estão representados na figuara e situados sobre a circunferância de centro na origem do plano complexo e raio igual a 2 u.c.
Nessas condições, z1 e z’2 é igual a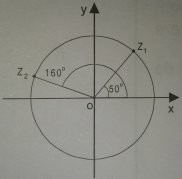
A) 2 (cos(250°) + isen(250°))
B) 4 (cos(210°) + isen(210°))
C) 4 (cos(110°) + isen(110°))
D) 2 (cos(210°) + isen(210°))
E) 4 (cos(250°) + isen(250°))
Solução: x1+x2 = 250°, pois esta
z1 . z’2 = p1.p2 [cos(x1+x2) + isen(x1+x2)]
z1 . z’2 = 2.2 [cos(250º) + isen(250º)]
z1 . z’2 = 4 [cos(250º) + isen(250º)]
Logo, a resposta correta é letra C.
46 - Estima-se que, para manter um ritmo de crescimento industrial e comercial desejável, uma determinada cidade terá seu consumo anual de energia elétrica aumentado em 0,5% ao ano. Se, atualmente, a cidade consome x kWh de energia por ano, transcorridos 7 anos e mantido esse ritmo de crescimento, o seu consumo anual de energia será de:
A) x . 10057 / 1014 kWh
B) x . 10057 / 1021 kWh
C) x . 1057 / 1021 kWh
D) x . 57 / 1021 kWh
E) x . 57 / 1014 kWh
Solução: A cidade consome, em porcentagem, 100x por ano e terá que aumentar, em porcentagem, 0,5x, que equivale a 100,5x % ou 1,005x
Essa questão é uma P.G de razão q = 1,005x, primeiro termo a1 = 1,005x e n = 7.
Substituindo os valores na formula geral da P.G: an = a1.qn-1
Teremos:
a7 = 1,005.(1,005)6
a7 = x.(1,005)7
a7 = x.(1005.10-3)7
a7 = x.(1005.10-3)7
a7 = x.10057.10-21
a7 = x.10057/1021
Logo, a resposta correta é B.
47 - O valor numérico da expressão [(x2 + y2)z/z-1] para x = 6, y =8 e z = 2,5 é igual a
A) 4.104
B) 2,5.105
C) 2,5.104
D) 4.104/5
E) 2,5.104/5
Solução:
[(62+82)2,5/(2,5)-1] =
[(36+64)5/2/(5/2)-1] =
[(100)5/2/(2/5)] =
[1005/2 . 5/2] =
(102)5/2 . 5/2 =
105 . 2,5 =
2,5 . 105.
Logo, a resposta correta é letra B
48 - Se P(x)=x2+bx+c, com b e c pertencentes a R, é um polinômio em x que possui uma raiz x1∈C-R, tal que x1 + x’1 = 8 e |x| = 5, então b+c é igual a
A) -3
B) 3
C) 13
D) 17
E) 21
Solução: P(x) = x2+bx+c e x1 + x’1 = 8
Podemos calcular a soma das raizes de um polinomio da seguinte forma:
S = -b/a = x1 + x’1 = 8 => -b/a = 8 =>-b = 8a => b = -8a
Podemos calcular o produto das raizes de um polinomio da seguinte forma:
P = x1.x’1 = c/a = |x1|.|x’1| = 5.5 = 25 => c = 25
Logo, b + c = -8 + 25 = 17, portanto, a resposta correta é letra D.
49 - Entre 26 condôminos de um edifício residencial, 5 deles devem ser escolhidos para ocupar os cargos de sindico, sub-síndico e três componentes do conselho fiscal. Com base nessa informação, pode-se afirmar que o número de resultados diferentes para essa escolha é igual a
A) 26!/ 6! 21!
B) 26!/ 3! 21!
C) 26!/ 6!
D) 26!/ 3!
E) 26!/ 21!
Solução: Primeiro vamos calcular os Arranjos para a eleição do sindico e subsindico (A ordem importa): An,p = n!/(p-n)!
A26,2 = 26!/(26-2)!
A26,2 = 26!/24!
Agora vamos calcular as combinações para o conseho fiscal (A ordem não importa): Cn,p = n!/[p!(n-1)!]
C24,3 = 24!/[3!(24-3)!]
C24,3 = 24!/3!21!
Agora vamos fazer as permutações entre arranjos e combinações, para saber quantas são as formas possiveis para compor os 5 cargos, para isso basta multiplicar: A26,2 . C24,3
A26,2 . C24,3 = 26!/24! . 24!/3!21! = 26! / (3!21!)
Logo,a resposta coreta é letra B.
50 - Para iluminar um ambiente durante t meses, uma pessoa possui duas opções:
I. Comprar uma lâmpada cujo preço é R$ 19,00 e seu consumo de energia elétrica corresponde a um custo mensal de R$ 0,80.
II. Comprar uma lâmpada cujo preço é R$ 3,00 e seu consumo de energia elétrica corresponde a um custo mensal de R$ 4,00.
Com base nessas informações, pode-se afirmar:
A) Se t = 3, então a opção I é a mais econômica.
B) Independente do valor de t, a opção II é a mais econômica.
C) Se t = 4, então a opção II faz com que se economize um total de R$ 5,00 em relação à opção I.
D) Se t > 5, então a opção I é a mais econômica.
E) Se t = 7, então a opção I faz com que se economize um total de R$ 5,00 em relação à opção II.
Solução: Primeiro vamos construir as equações:
I: y1 = 0,8t + 19
II: 4t + 3
Agora vamos testar as opções:
Letra (A): y1 = 0,8.3 + 19 = 21,4 e y2 = 4.3 + 3 = 15
Letra (B): Falsa, pois para t > 5 a opção um é mais vantajosa qua a opção dois
Letra (C): y1 = 0,8.4 + 19 = 22,2 e y2 = 4.4 + 3 = 19
Letra (D): y1 = 0,8.6 + 19 = 23,8 e y2 = 4.6 + 3 = 27
Letra (E): y1 = 0,8.7 + 19 = 26,2 e y2 = 4.7 + 3 = 31
Logo, a resposta correta é letra D.



0 Comentários