1 – Qual é o número obtido calculando 2005 − 205 + 25 − 2 ?
(A) 1 773 (B) 1 823 (C) 1 827 (D) 1 873 (E) 2 237
Resposta: A expressão contém apenas adições e subtrações, por isso podemos efetuar essas operações em qualquer ordem. A escolha sobre qual a melhor ordem é apenas uma questão de conveniência. Por exemplo, podemos efetuar primeiro as subtrações, escrevendo:
2005 − 205 + 25 − 2 = (2005 − 205) + (25 − 2) = 1800 + 23 = 1823 .
2 – Guilherme está medindo o comprimento de um selo com um pedaço de uma régua, graduada em centímetros, como mostra a figura. Qual é o comprimento do selo?

(A) 3 cm (B) 3,4 cm (C) 3,6 cm (D) 4 cm (E) 4,4 cm
Resposta: Por leitura direta da figura, vemos que uma extremidade do selo está na marca de 20 cm e a outra na marca de 16,6 cm. O comprimento do selo é a diferença entre estes dois valores, ou seja, 20 − 16,6 = 20,0 − 16,6 = 3,4 cm.
3 – Margarida viu no quadro-negro algumas anotações da aula anterior, um pouco apagadas, conforme mostra a figura. Qual é o número que foi apagado?

(A) 9 (B) 10 (C) 12 (D) 13 (E) 15
Resposta: Denotemos por a o numerador da fração que aparece no quadro negro. Temos a/3 = 5, donde a = 3 x 5 = 15. Por outro lado, a = 2 x 12 − x onde x representa o número apagado. Portanto 2 x 12 − x = 15 , ou seja 24 − x = 15 . Logo x = 9.
4 – O piso de uma cozinha foi revestido de ladrilhos brancos e pretos, conforme a figura. Cada ladrilho branco custou R$ 2,00 e cada ladrilho preto custou R$ 3,00. Quanto foi gasto na compra dos ladrilhos?

(A) R$ 126,00 (B) R$ 144,00 (C) R$ 174,00 (D) R$ 177,00 (E) R$ 189,00
Resposta: Na figura temos um retângulo de 9 ladrilhos no comprimento e 7 na largura, o que dá um total de 9 x 7 = 63 ladrilhos, dos quais 12
são brancos. Então o número de ladrilhos pretos é 63 − 12 = 51. Logo o custo total do piso é 12 x 2 + 51 x 3 = 24 + 153 = 177 reais.
5 – As duas peças de madeira a seguir são iguais.

Pode-se juntar essas duas peças para formar uma peça maior, como mostra o seguinte exemplo.
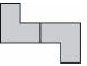
Qual das figuras abaixo representa uma peça que NÃO pode ser formada com as duas peças dadas?
|
(A) |
|
(B) |
|
(C) |
|
(D) |
|
(E) |
|
Resposta: Os desenhos abaixo mostram como juntar as duas peças para obter as alternativas (A), (B), (C) e (D).

Apenas a alternativa (E) não pode ser obtida juntando as duas peças, como se pode verificar diretamente por tentativas.
6 – Marina, ao comprar uma blusa de R$ 17,00, enganou-se e deu ao vendedor uma nota de R$ 10,00 e outra de R$ 50,00. O vendedor, distraído, deu o troco como se Marina lhe tivesse dado duas notas de R$ 10,00. Qual foi o prejuízo de Marina?
(A) R$ 13,00 (B) R$ 37,00 (C) R$ 40,00
(D) R$ 47,00 (E) R$ 50,00
Resposta: Marina, ao dar 60 reais para pagar uma conta de 17 reais, deveria receber 60 − 17 = 43 reais de troco, mas recebeu somente 20 − 17 = 3 reais. Logo, seu prejuízo foi de 43 − 3 = 40 reais.
Uma outra maneira de resolver o problema é notar que, ao confundir uma nota de 10 reais com uma de 50 reais, Marina teve um prejuízo de 50 − 10 = 40 reais. Esta solução mostra que o prejuízo de Marina não depende do preço da blusa.
7 – A capacidade do tanque de gasolina do carro de João é de 50 litros. As figuras mostram o medidor de gasolina do carro no momento de partida e no momento de chegada de uma viagem feita por João. Quantos litros de gasolina João gastou nesta viagem?
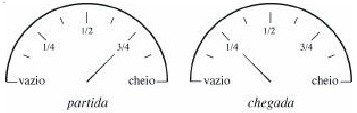
(A) 10 (B) 15 (C) 18 (D) 25 (E) 30
Resposta: As figuras mostram que o tanque de gasolina do carro continha 3/4 de sua capacidade no momento de partida e 1/4 no momento de chegada. Deste modo, João gastou 3/4 − 1/4 = 1/2 do tanque na viagem. Como o tanque tem capacidade para50 litros, isto quer dizer que João gastou 50 x 1/2 = 25 litros de gasolina na viagem. Note que esta última conta pode serpensada como “João gastou meio tanque de gasolina e a metade de 50 é 25”.
8 – Daniela quer cercar o terreno representado pela figura. Nessa figura dois lados consecutivos são sempre perpendiculares e as medidas de alguns lados estão indicadas em metros. Quantos metros de cerca Daniela terá que comprar?
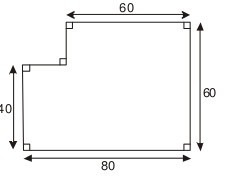
(A) 140 (B) 280 (C) 320 (D) 1 800 (E) 4 800
Resposta: Precisamos calcular o perímetro do polígono mostrado na figura, ou seja, queremos achar AB + BC + CD + DE + EF + FA . Nestasoma conhecemos as parcelas AB = 80 , BC = 60 , CD = 60 e FA = 40 , e assimnosso problema é achar o comprimento de DE e EF. O ponto G na figura é construídoprolongando-se o lado DE. Obtemos então os dois retângulos AGEF e BCDG. LogoEF = AB− CD = 80 − 60 = 20 e DE = BC − AF = 60 − 40 = 20. Assim, o perímetro pedido é80 + 60 + 60 + 20 + 20 + 40 = 280 metros. Para justificar o raciocínio acima, notamos que AGEF e BCDG são retângulos porque dois quaisquer de seus lados consecutivos sãoperpendiculares. Como os lados opostos de um retângulo têm a mesma medida, podemos calcular EF e DE mais detalhadamente como EF = AG = AB − BG = AB − CD = 80 − 60 = 20 eDE = DG − EG = BC − AF − 60 − 40 = 20.
As questões 9 e 10 referem-se ao Campeonato Brasileiro de Futebol 2005. O Campeonato 2005 é disputado por 22 times. Cada time enfrenta cada um dos outros duas vezes, uma vez em seu campo e outra no campo do adversário.
9 – Quantas partidas serão disputadas por cada time?
(A) 40 (B) 41 (C) 42 (D) 43 (E) 44
Resposta: Como há 22 times no campeonato e cada time só não enfrenta a si próprio, então ele joga 21 vezes (com os outros 21 times)em seu campo e mais 21 vezes nos campos dos adversários. No total, cada time disputa 21 + 21 = 42 partidas.
10 – Um time ganha 3 pontos por vitória, 1 ponto por empate e nenhum ponto em caso de derrota. Até hoje cada time já disputou 20 jogos. Se um desses times venceu 8 jogos e perdeu outros 8 jogos, quantos pontos ele tem até agora?
(A) 23 (B) 25 (C) 26 (D) 27 (E) 28
Resposta: Como o time disputou 20 jogos, venceu 8 e perdeu 8, o número de empates é: 20 − 8 − 8 = 4 . Logo, o time obteve 8 x 3 = 24pontos com as vitórias e 4 x 1 = 4 pontos com os empates. Portanto, o time obteve 24 + 4 = 28 pontos (o time não ganha pontosquando perde).
11 – Qual é a medida do menor ângulo formado pelos ponteiros de um relógio quando ele marca 2 horas?
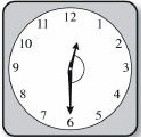
(A) 30o (B) 45o (C) 60o (D) 75o (E) 90o
Resposta: Os números (de 1 a 12) no mostrador do relógio dividem a circunferência em 12 partes iguais, e a cada uma corresponde umângulo central de 360o÷12 = 30o. Quando o relógio marca 2 horas, o ângulo formado pelos ponteiros corresponde à soma dedois ângulos de 30o cada, logo é igual a 2 x 30o = 60o.
12 – Uma folha quadrada foi cortada em quadrados menores da seguinte maneira: um quadrado de área 16 cm2, cinco quadrados de área 4 cm2 cada um e treze quadrados de área 1 cm2 cada um. Qual era a medida do lado da folha, antes de ela ser cortada?
(A) 3 cm (B) 4 cm (C) 5 cm (D) 7 cm (E) 8 cm
Resposta: Lembre que a área de um quadrado de lado L é igual a L2 ; deste modo, se conhecemos aárea a de um quadrado então seu lado é a √A área da folha cortada é a soma das áreas dosquadrados menores, que é 16+5 x 4+13 x 1 = 49 cm2. Logo, antes de ser cortada, a folha tinha lado 49 = 7 cm.
Outra solução deste problema é notar que os quadrados do enunciado podem ser agrupados de modo a formar um quadrado maior de lado 7.
13 – Um cubo de madeira tem 3 cm de aresta. Duas faces opostas foram pintadas de amarelo e as outras quatro faces foram pintadas de verde. Em seguida o cubo foi serrado em 27 cubinhos de 1 cm de aresta, conforme indicado no desenho.
Quantos cubinhos têm faces pintadas com as duas cores?
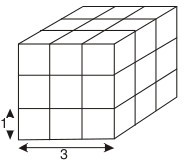
(A) 16 (B) 18 (C) 20 (D) 22 (E) 24
Resposta: Num cubo, duas faces são adjacentes quando têm uma aresta comum e opostas quando não têm aresta comum. No caso,duas faces opostas do cubo foram pintadas de amarelo e as outras quatro de verde, ou seja, cada face verde é adjacente àsduas amarelas. Em cada face amarela do cubo, 9 cubinhos têm uma face amarela. Desses 9 cubinhos, apenas o do centro nãotem uma face verde. Logo em cada face amarela temos 8 cubinhos com faces verde e amarela. Como o cubo tem duas facesamarelas, o número total de cubinhos que têm faces com duas cores é 8 + 8 = 16.
14 – Qual das expressões abaixo tem como resultado um número ímpar?
(A) 7 x 5 x 11 x 13 x 2 (B) (2005 − 2003) x (2004 + 2003)
(C) 7 + 9 + 11 + 13 + 15 + 17 (D) 52 + 32
(E) 3 x 5 + 7 x 9 + 11 x 13
Resposta: Como os números envolvidos são pequenos, a questão pode ser resolvida efetuando os cálculos indicados e verificando aparidade do resultado:
(A) 7 x 5 x 11 x 13 x 2 = 10010 que é par
(B) (2005 − 2003) x (2004 + 2003) = 2 x 4007 = 8014 que é par
(C) 7 + 9 + 11+ 13 + 15 + 17 = 72 que é par
(D) 5 2 + 3 2 = 25 + 9 = 34 que é par
(E) 3 x 5 + 7 x 9 + 11 x 13 = 15 + 63 + 143 = 221 que é ímpar
Por outro lado, usando seguintes fatos sobre números inteiros
par + par = par
par + ímpar = ímpar
ímpar + ímpar = par
(qualquer número) × par = par
ímpar × ímpar = ímpar
podemos argumentar como se segue. Os resultados de (A) e (B) são pares, pois ambos contêm o fator 2. Os resultados de (C) e (D) são pares pois são somas de um número par de parcelas ímpares. Finalmente o resultado de (E) é ímpar pois é a soma de um número ímpar de parcelas ímpares. Note que este argumento não depende do fato dos números envolvidos serem grandes ou pequenos.
15 – Os bilhetes de uma rifa são numerados de 1 000 a 9 999. Marcelo comprou todos os bilhetes nos quais o algarismo sete aparece exatamente três vezes e o zero não aparece. Quantos bilhetes Marcelo comprou?
(A) 32 (B) 36 (C) 45 (D) 46 (E) 48
Resposta: Os números nos bilhetes comprados por Marcelo são da forma 777X, 77X7, 7X77 ou X777, onde X representa algum dos oitoalgarismos 1, 2, 3, 4, 5, 6, 8 e 9. Em cada um desses casos, há 8 possibilidades para os números dos bilhetes. Por exemplo,no primeiro caso, temos os seguintes oito números: 7771, 7772, 7773, 7774, 7775, 7776, 7778 e 7779. Portanto, o número debilhetes comprados por Marcelo é 4 x 8 = 32.
16 – Rosa e Maria começam a subir uma escada de 100 degraus no mesmo instante. Rosa sobe 10 degraus a cada 15 segundos e Maria sobe 10 degraus a cada 20 segundos. Quando uma delas chegar ao último degrau, quanto tempo faltará para a outra completar a subida?
(A) meio minuto (B) 40 segundos (C) 45 segundos
(D) 50 segundos (E) 1 minuto
Resposta: Como 100 degraus = 10 x 10 degraus, Rosa gastará 15 x 10 = 150 segundos para chegar ao último degrau da escada. Do mesmo modo, Maria levará 20 x 10 = 200 segundos para atingir o topo da escada. Assim, quando Rosa terminar de subir aescada, faltarão 200 − 150 = 50 segundos para Maria completar a subida.
17 – Valdemar vai construir um muro de 2 m de altura por 7m de comprimento. Ele vai usar tijolos de 5 cm de altura por 20 cm de comprimento unidos por uma fina camada de cimento, conforme indicado na figura. Sabendo que os tijolos são vendidos em milheiros, quantos milheiros Valdemar vai ter que comprar para construir o muro?
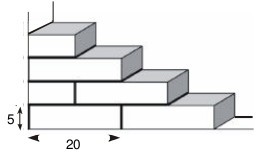
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Resposta: Sabemos que 1 m = 100 cm. A altura do muro é igual a 2 m, ou seja, 200 cm, e a altura de cada tijolo é de 5 cm. Logo, serãonecessárias cerca de 200 ÷ 5 = 40 camadas horizontais de tijolos para atingir a altura do muro. O comprimento do muro é de7 m, ou seja, 700 cm e o comprimento de um tijolo é de 20 cm. Assim, devem ser colocados em cada camada horizontal domuro cerca de 700 ÷ 20 = 35 tijolos. Levando em conta a espessura da camada de cimento, podemos estimar que o númerototal de tijolos necessários é 40 x 35 = 1400. Logo Valdemar vai precisar comprar dois milheiros de tijolos.
18 – Caio e Sueli começaram, separadamente, a guardar moedas de R$ 1,00 em janeiro de 2004. Todo mês Caio guardava 20 moedas e Sueli guardava 30 moedas. Em julho de 2004 e nos meses seguintes, Caio não guardou mais moedas, enquanto Sueli continuou a guardar 30 por mês. No final de que mês Sueli tinha exatamente o triplo do número de moedas que Caio guardou?
(A) agosto (B) setembro (C) outubro (D) novembro (E) dezembro
Resposta: De janeiro a junho há 6 meses. Portanto, Caio economizou 6 x 20 = 120 moedas até junho. O triplo de 120 é 3 x 120 = 360 . ComoSueli continuou guardando 30 moedas por mês, ela conseguiu guardar 360 moedas após 360 ÷ 30 = 12 meses, ou seja, emdezembro de 2004.
19 – Para testar a qualidade de um combustível composto apenas de gasolina e álcool, uma empresa recolheu oito amostras em vários postos de gasolina. Para cada amostra foi determinado o percentual de álcool e o resultado é mostrado no gráfico abaixo. Em quantas dessas amostras o percentual de álcool é maior que o percentual de gasolina?
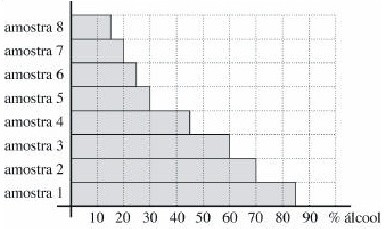
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Resposta: As amostras cujo percentual de álcool é maior que o de gasolina são aquelas que contêm mais de 50% de álcool. No gráfico, estasamostras correspondem àquelas cuja barra horizontal ultrapassa a marca de 50%, que são as amostras de número 1, 2 e 3.
20 – O aniversário de Carlinhos é no dia 20 de julho. Em agosto de 2005, ao preencher uma ficha em sua escola, Carlinhos inverteu a posição dos dois últimos algarismos do ano em que nasceu. A professora que recebeu a ficha disse: – Carlinhos, por favor, corrija o ano de seu nascimento, senão as pessoas vão pensar que você tem 56 anos ! Qual é a idade de Carlinhos?
(A) 11 anos
(B) 12 anos
(C) 13 anos
(D) 14 anos
(E) 15 anos
Resposta: Como estamos em agosto de 2005, Carlinhos já fez seu aniversário este ano. Assim, ao inverter os dois últimos algarismos do ano em que nasceu, ele escreveu na ficha o ano 2005 − 56 = 1949 . Ele deveria então ter escrito 1994, que é o verdadeiro ano do seu nascimento. Portanto Carlinhos tem 2005 − 1994 = 11 anos.













0 Comentários