Definição: Uma função f:R→R chama-se quadrática quando existem três números reais a, b e c tal que f(x) = ax2 + bx + c, com a ≠ 0.
Exemplos:
f(x) = x2 - 2x + 1 (a = 1 , b = -2 , c = 1);
y = -x2 (a = -1 , b = 0 , c = 0).
y = -2x2 + 2x (a = -2 , b = 2 , c = 0)
y = -(1/2)x2 – 1/4 (a = -1/2 , b = 0 , c = 1/4)
Zeros da função: chama-se zeros ou raízes da função polinomial do 2º grau, os números reais x tais que f(x) = 0. Então as raízes da função f(x) = ax2 + bx + c, são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
Exemplo: Vamos calcular as raízes da função f(x) = x2 - 2x + 1.
f(x) = 0 => x2 - 2x + 1 = 0
Primeiro vamos calcular o valor de ?.
Δ =b2 – 4.a.c
Δ = (-2)2 – 4.1.1
Δ = 4 – 4 = 0
Sabemos que: x = (-b±√Δ)/2.a
x = (-2±√0)/2.1 = (-2±0)/2
x1 = x2 = -2/2 = 1
Portanto a raiz da função é 1.
Propriedades do gráfico de y = ax2 + bx + c
1) O gráfico da função do 2º grau é sempre uma parábola de eixo vertical.
|
|
|
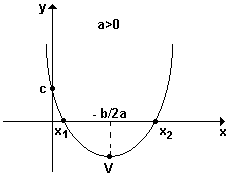
2) se a > 0 a parábola tem um ponto de mínimo e a concavidade é voltada para cima;
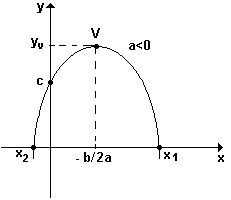
3) se a < 0 a parábola tem um ponto de máximo e a concavidade é voltada para baixo;
4) o vértice da parábola é o ponto V(xv , yv) onde: V(xv = - b/2a; yv = - Δ/4a), onde Δ = b2 – 4ac;
5) a parábola intercepta (corta) o eixo dos x nos pontos de abcissas x' e x'', que são as raízes da equação ax2 + bx + c = 0;
6) a parábola intercepta o eixo dos y no ponto (0 , c);
7) o eixo de simetria da parábola é uma reta vertical de equação xv = - b/2a;
8) ymax = -Δ/ 4a ( a ≠ 0 ) e ymin = -Δ/4a (a ≠ 0);
9) Im(f) = {y∈R; y < -Δ/4a} (a ≠ 0) ou Im(f) = {y∈R; y > -Δ/4a} (a≠0);
10) Forma fatorada: sendo x1 e x2 as raízes da de f(x) = ax2 + bx + c, então ela pode ser escrita na forma fatorada a seguir: y = a (x - x1).(x – x2);
Propriedades
|
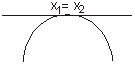
Se Δ < 0 ⇒ Não há raízes reais. |
|
|
|
|
|
Se Δ = 0 ⇒ Duas raízes reais e iguais. |
|
|
|
|
|
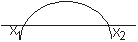
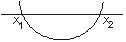
Se Δ > 0 ⇒ Duas raízes reais e diferentes |
|
|
|
|
Reconhecimento gráfico
O gráfico da função y = ax2 é uma Parábola com vértice (ponto extremo)
na origem, tendo para eixo de simetria o próprio eixo y.
Se a > 0, a parábola tem concavidade voltada para cima.
Se a < 0, a parábola tem concavidade voltada para baixo.
A abertura da parábola é tanto maior quanto mais próximo de zero for o valor de a.
|
Valor Máximo |
|
|
Se a < 0, o vértice é o ponto mais alto do gráfico. Enquanto x varia de -∞ a +∞, y varia de -∞ a yv. Portanto, o maior valor que o trinômio y = ax2 + bx + c pode assumir é yv = - Δ/4a. Isso acontece quando x é igual a xv = -b/2a. |
|
|
Valor Mínimo |
|
|
Se a > 0, o vértice é o ponto mais baixo do gráfico. Enquanto x varia de -∞ a +∞, y varia de yv a +∞. Portanto, o menor valor que o trinômio y = ax2 + bx + c pode assumir é yv = - Δ/4a. Isso acontece quando x é igual a xv = -b/2a. |
|
Construção da Parábola: É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y), conforme mostrado abaixo:
1 – O valor do coeficiente a define a concavidade da parábola;
2 – Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
3 – O vértice V(-b/2a, -Δ/4a) indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
4 – Para x = 0 , temos y = a · 02 + b · 0 + c = c; então (0, c) é o ponto em que a parábola corta o eixo dos y.
5 – A reta, paralela ao eixo dos y, que passa por V, é o eixo de simetria da parábola;
6 – Agora basta construir a parabola;
Exercício Resolvido:
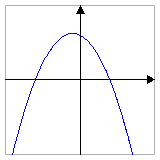
1 – Construa o gráfico da função f(x)= -x2 – x + 6.
Solução:
A) Como a < 0, a concavidade é voltada para baixo;
B) Vamos calcular os zeros da função:
Vamos marcar no gráfico os pares (-3,0) e (2,0);
C) Vamos calcular o vértice:
Vamos marcar no gráfico o par
D) Vamos calcular f(0): f(0) = -02 – 0 + 6 = 6
Vamos marcar no gráfico o par (0,6);
E) Agora basta construir a parabola:
2 – Com relação à função f(x) = 3x2 – 5x + m2 – 9, sabe-se que f(0) = 0. Calcule o valor de m.
Solução: f(0) = 0, então, x = 0 e y = 0. A função f(x) = 3x2 – 5x + m2 – 9 pode ser escrita assim: y = 3x2 – 5x + m2 – 9, agora basta fazer as substituições:
f(x) = 3x2 – 5x + m2 – 9
f(0) = 3.02 – 5.0 + m2 – 9
0 = m2 – 9
m2 = 9
m = √9
m = – 3 ou + 3



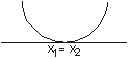

0 Comentários