Uma função y = f(x) é injetora quando elementos distintos do seu domínio possuem imagens distintas, isto é: 

Sejam x₁ e x₂ ∈ℝ:

x₁ ≠ x₂ ⇔ f(x₁) ≠ f(x₂) 

ou 

f(x₁) = f(x₂) ⇒ x₁= x₂; 

Exemplos: 

1. A função y = 5x - 2 é injetora pois dados x₁ ≠ x₂ podemos escrever f(x₁) - f(x₂) ≠ 0. Portanto, (5x₁ - 2) - (5x₂ -2) = 5 (x₁ - x₂) ≠ 0, pois x₁ ≠ x₂.
2. A função f:R → R definida por f(x) = x² + 3 não é injetora, pois para x = 1 temos f(1) = 4 e para x = -1 temos f(-1) = 4.
3. A função f:R → R definida por f(x) = x (identidade) é injetora, para qualquer domínio e contradomínio.

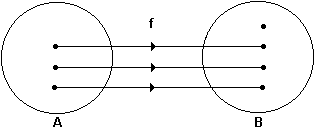
Observando o diagrama, abaixo, vemos que os elementos do domínio estão ligados a um e somente um elemento do contradomínio, isto é, não existem elementos em A com imagens iguais. Portanto, se uma função f: A ⇒ B é injetora, então n(A) ≤ n(B) 

Uma função sobrejetora é aquela cujo conjunto imagem é igual ao contradomínio, ou seja, todo elemento do dominio estão ligados a, pelo menos, um elemento do contradomínio. Note também que não SOBRAM elementos no contradomínio.

Definição: Seja a função f, com domínio em A e contradomínio em B e lei de formação igual a f(x) = y. A função é sobrejetora se, e somente se, para todo elemento (y) de B existir, pelo menos, um elemento (x) de A, tal que f(x) = y. Em notação algebrica:

∀y∈B; ∃ x∈A| f(x) = y 

Exemplos: 

1. A função dada por y = 3x + 2 de R em R é sobrejetora pois para cada valor de x do domínio, existe pelo menos um correspondente (imagem) no contradomínio.
2. A função f:R → R definida por f(x) = 2^x não é sobrejetora, pois o número -1 é elemento do contradomínio R e não é imagem de qualquer elemento do domínio.

Observando o diagrama, abaixo, vemos que todos os elementos do contradomínio estão ligados a algum elemento do domínio, isto é, não sobram elementos no contradomínio. Portanto, se uma função f: A ⇒ B é sobrejetora, então n(A) ≥ n(B).

Uma função é dita bijetora, quando é ao mesmo tempo, injetora e sobrejetora. Dessa forma, podemos dizer que uma função é bijetora quando todo elemento do domínio (A) tem correspondente no contradomínio (B) e ao mensmo tempo, elementos distintos do domínio tem imagens diferentes.

Exemplos: 

1. A função f:R → R dada por f(x)=2x é bijetora, pois é ao mesmo tempo injetora e sobrejetora;
2. A função f : R→ R definida por y = 4x - 1 é uma função bijetora, pois é ao mesmo tempo injetora e sobrejetora.

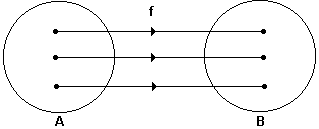
Observando o diagrama, abaixo, vemos que todos os elementos do domínio estão ligados a algum elemento do contradomínio e não existem elementos em A com imagens iguais. Portanto, se uma função f: A -> B é bijetora então n(A) = n(B)

Exercícios resolvidos

1) Verifique se a função f: Q→Q definida por f(x) = x² + 1 é injetora, sobrejetora, bijetora. 

Solução: Se f é injetora, f(x₁) = f(x₂) ⇒ x₁ = x₂. Daí, x₁² + 1 = x₂² + 1 ⇒ x₁² = x₂², logo, a função é injetora. 

A função f não é sobrejetora pois, para f(x) = 0 não existe x tal que x² + 1 = 0. Como f não é sobrejetora ela também não pode ser bijetora.

Logo, ela é apenas injetora.

2) Determine se a função f: Z→Z definida por f(x) = x², é injetora.

Solução: A função f(x) = x² não é injetora pois, por exemplo 1 ≠ -1 mas f(1) = f(-1) = 1.

3) Determine se a função f : Z→Z definida por f(x) = x + 1, é injetora.

Solução: A função f(x) = x + 1 é injetora pois sempre x₁ ≠ x₂, então, x₁ + 1 ≠ x₂ + 1.

4) Determine se a função f: Z→Z definida por f(x) = x², é sobrejetora.

Solução: A função f(x) = x² não é sobrejetora pois, por exemplo, para f(x) = -1 não existe x tal que x² = -1 (Existem elementos no contradomínio sem correspondente no conjunto domínio). 

5) Determine se a função f: Z→Z definida por f(x) = x + 1, é sobrejetora.

Solução: A função f(x) = x + 1 é sobrejetora, pois para todo inteiro y existe um inteiro x tal que x + 1 = y.

6) Determine se a função f: Z→Z definida por f(x)=x+1, é bijetora.

Solução: A função f(x) = x + 1 é bijetora pois, como vimos acima, nas questões 3 e 5, a função é injetora e sobrejetora.

7) Considere três funções f, g e h, tais que:

• A função f atribui a cada pessoa do mundo, a sua idade;

• A função g atribui a cada país, a sua capital;

• A função h atribui a cada número natural, o seu dobro.

Podemos afirmar que, das funções dadas, são injetoras:

a) f, g e h 

b) f e h 

c) g e h 

d) apenas h 

e) n.d.a.

Solução: Sabemos que numa função injetora, elementos distintos do domínio, possuem imagens distintas, ou seja: x₁ ≠ x₂ ⇔ f(x₁) ≠ f(x₂) . Logo, podemos concluir que: f não é injetora, pois duas pessoas distintas podem ter a mesma idade. g é injetora, pois não existem dois países distintos com a mesma capital. h é injetora, pois dois números naturais distintos, possuem os seus dobros também distintos. Assim é que concluímos que a alternativa é a de letra C.

Exercícios propostos

1) Verifique em cada caso se a função é injetora, sobrejetora, bijetora ou não injetora e nem sobrejetora.

a) f(x) = -2x + 1

b) f(x) = x² + 3

c) f(x) = -2

d) f(x) = -2x³

e) f(x) = x⁹ 

f) f(x) = x⁴ + 2

2) Considere três funções f, g e h, tais que:

 I - A função f atribui a cada pessoa do mundo, o seu nome;

II - A função g atribui a cada país, o seu idioma;

III - A função h atribui a cada número real, o seu triplo.

Podemos afirmar que, das funções dadas, são bijetoras:

a) f, g e h 

b) f e h 

c) g e h 

d) f e g 

e) n.d.a.