1 - Expoentes irracionais em álgebra, as potências inteiras e racionais de um número b estão definidas por:

b_n = bxbx...xb (n fatores),

b^-n = 1/bⁿ,

b⁰ = 1 e

b^p/q = ^q√b^p = (^q√b)^p = b^-p/q = 1/ b^p/q.

 

Se b for negativo, então algumas das potências fracionárias de b terão valores imaginários; por exemplo, (-2)² = √-2. para evitar esta complicação, vamos supor que, b ≥ 0 mesmo que não seja estabelecido explicitamente. Observe que as definições precedentes não incluem potências irracionais de b, tais como 2^pi, 2^√2, 2^-√7. 

Há vários métodos para definir potências irracionais. uma abordagem é definir potências irracionais de b como limite de potências racionais. por exemplo, para definir 2^pi devemos começar com a representação decimal de pi, isto é, 3,1415926, desta decimal, podemos formar uma seqüência de números racionais que ficam cada vez mais próximos de pi isto é, 3,1; 3,14; 3,141; 3,1415; 3,14159 e a partir destes podemos formar uma sequência de potências racionais de 2: 2^3,1, 2^3,14, 2^3,141, 2^3,1415, 2^3,14159 uma vez que os expoentes dos termos desta sequência tendem a um limite pi, parece plausível que os próprios termos tendam a um limite; sendo assim, é razoável definir 2^pi como sendo este limite, a tabela abaixo fornece evidência numérica de que a sequência, na realidade, tem um limite e para quatro casas decimais, o valor deste limite é 2^pi ≈ 8,8250. em geral, para qualquer expoente irracional p e número positivo b, podemos definir b^p como o limite de potências racionais de b, criadas pela expansão decimal de p.

x = 3 ⇒ 2x = 8 x = 3,1415 ⇒ 2x = 8,824411 x = 3,1414592 ⇒ 2x = 8,824974 x = 3,1 ⇒ 2x = 8,574188

x = 3,141 ⇒ 2x = 8,821353 x = 3,14 ⇒ 2x = 8,815241 x = 3,14159 ⇒ 2x = 8,824962

 

2 - A família de funções exponenciais

Uma função da forma f (x) = b^x , onde b > 0 e b ≠ 1, é chamada de função exponencial de base b, cujos exemplos são f(x) = 2^x , f(x) = (½)^x, f(x) = 2^pi.

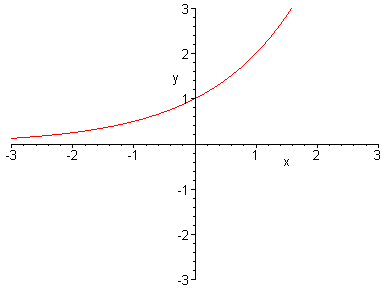
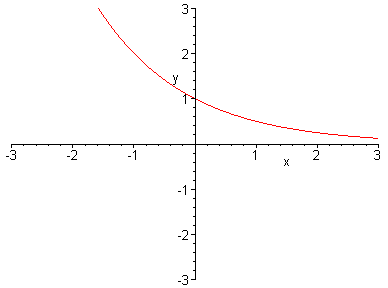
Note que uma função exponencial tem uma base constante e um expoente variável. assim as funções tais como f(x) = x² e f(x) = xⁿ não seriam classificadas como funções exponenciais, uma vez que elas tem uma base variável e um expoente constante. Pode ser mostrado que as funções exponenciais são contínuas e têm um dos dois aspectos básicos mostrados na figura 1, dependendo de se 0 < b < 1 ou b > 1. Já a figura 2 mostra os gráficos de algumas funções exponenciais específicas.

 

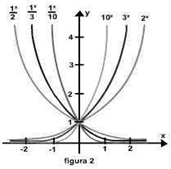
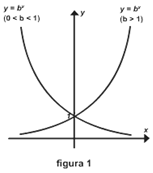
Observação: se b = 1, então a função b^x é constante, uma vez que b^x = 1^x = 1. Este caso não é de nosso interesse aqui, assim o excluímos da família das funções exponenciais.

 

3 - Equações exponenciais chamamos de equações exponenciais toda equação na qual a incógnita aparece em expoente.

Exemplos de equações exponenciais:

3^x = 81 (a solução é x = 4);

2^x-5=16 (a solução é x = 9);

16^x-4^2x-1-10=2^2x-1 (a solução é x=1) e

3^2x-1 - 3^x - 3^x-1 + 1 = 0 (as soluções são x’ = 0 e x’’ = 1).

 

3.1 - Para resolver equações exponenciais, devemos realizar dois passos importantes:

1º) redução dos dois membros da equação a potências de mesma base;

2º) aplicação da propriedade: a^m = aⁿ ⇒ m = n (a ≠ 1 e a > 0).

 

4 - Exercícios resolvidos:

1) 3^x = 81. Solução: como 81 = 3⁴, podemos escrever 3^x = 3⁴ e daí, x = 4.

2) 9^x = 1. Solução: 9^x = 1 ⇒ 9^x = 9⁰; logo x=0.

3) (3/4)^x = 81/256. Solução: (3/4)^x = 3⁴/4⁴ ⇒ x = 4.

4) 3^x = ⁴√27. Solução: 3^x = ⁴√3³ ⇒ 3^x = 3^3/4 ⇒ x = 3/4 .

5) 2^3x-1 = 32^2x. Solução: 2^3x-1 = 32^2x ⇒ 2^3x-1 = (2⁵)^2x ⇒ 2^3x-1 = 2^10x ⇒ 3x - 1 = 10 ⇒ x = -1/7.

6) Resolva a equação 3^2x – 6.3^x – 27=0.

Solução: para resolver esta equação vamos fazer uma transformação. Observe que 3^2x = (3^x)². Feito isso, basta substituir 3^x por y na equação, ou seja, (I) 3^x = y. Substituindo na equação temos que: y² – 6y – 27 = 0; resolvendo a equação temos que: y’= -3 e y’’ = 9, para achar o valor de x, devemos voltar os valores para a equação (I), substituindo os valores encontrados em I:

y’=-3 ⇒ 3^x’ = -3 ⇒ não existe x’, pois potência de base positiva é positiva;

y’’= 9 ⇒ 3^x’’ = 9 ⇒ 3^x’’ = 3² ⇒ x’’=2. Portanto a solução é x = 2.

 

6 - gráfico cartesiano da função exponencial temos 2 casos a considerar: Quando a > 1 e quando a < 1.

Exemplos

1º) y = 2^x (nesse caso, a = 2, logo a > 1) atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos a tabela e o gráfico abaixo:

x	-2	-1	0	1	2
y	1/4	½	1	2	4

 

 

 

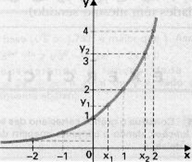
2º) y = (1/2)^x (nesse caso, a = 1/2, logo a < 1) atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos a tabela e o gráfico abaixo:

x	-2	-1	0	1	2
y	4	2	1	1/2	1/4

 

 

 

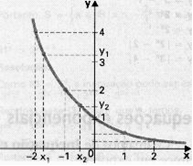
Nos dois exemplos, podemos observar que

• O gráfico nunca intercepta o eixo horizontal; a função não tem raízes;

• O gráfico corta o eixo vertical no ponto (0,1);
• Os valores de y são sempre positivos (potência de base positiva é positiva), portanto o conjunto imagem é im=IR+. Além disso, podemos estabelecer o seguinte:

 

a > 1	a<1
f(x) é crescente e Im(f) = IR+, para quaisquer x1 e x2 do domínio: x2 > x1 ⇒ y2 > y1 (as desigualdades têm mesmo sentido)	f(x) é decrescente e Im(f) = IR+, para quaisquer x1 e x2 do domínio: x2 > x1 ⇒ y2 < y1 (as desigualdades têm sentidos diferentes)

7 - inequações exponenciais chamamos de inequações exponenciais toda inequação na qual a incógnita aparece em expoente.

 

7.1- para resolver inequações exponenciais, devemos realizar dois passos importantes:

1º) Redução dos dois membros da inequação a potências de mesma base;

2º) Aplicação da propriedade:

 

a > 1	a < 0
am > an ⇒ m > n (as desigualdades têm mesmo sentido)	am > an ⇒ m < n (as desigualdades têm sentidos diferentes)

7.2 Exemplos de inequações exponenciais:

1) Resolva a inequação: 4^x-1 + 4^x – 4^x+1 > -11/4.

Solução: A inequação pode ser escrita da seguinte forma: (4^x/4¹) + 4^x – 4^x.4¹ > -11/4. Agora multiplicando ambos os membros por 4, temos: 4^x.(4/4) + 4.4^x – 4^x.4² > -11, efetuando os devidos cálculos, chegamos a, 4^x.1 + 4.4^x – 4^x.16 > -11 ⇒ 4^x + 4.4^x – 16.4^x > -11. Aplicando a propriedade distributiva (Colocando o fator comum em evidência) teremos (1+4+16).4^x > -11 ⇒ -11.4^x > -11 ⇒ 4^x > -11/-11. Aqui temos que ter bastante atenção para não errar o sinal. Multipliquemos a desigualdade por (-1), observe que, o sinal de '>' deve ser trocado por '<' daí, 11.4^x < 11 ⇒ 4^x < 11/11 ⇒ 4^x < 1, como 1 = 4⁰ (pois, todo número real não nulo elevado ao expoente zero é igual a um). Concluimos que x < 0. S = IR_- (Reais negativos).

 

2)Resolva as inequações abaixo:

a) 3^x > 81. (Solução: x > 4);

b) 2^2x-2 ≤ 2^x.x-1. (Solução: Valida para todo x real);

c) (4/5)^x ≤ (4/5)^-3. (Solução: x≤ -3);

d) 25^x – 150.5 + 3125. (Solução: 2).