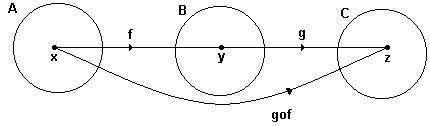
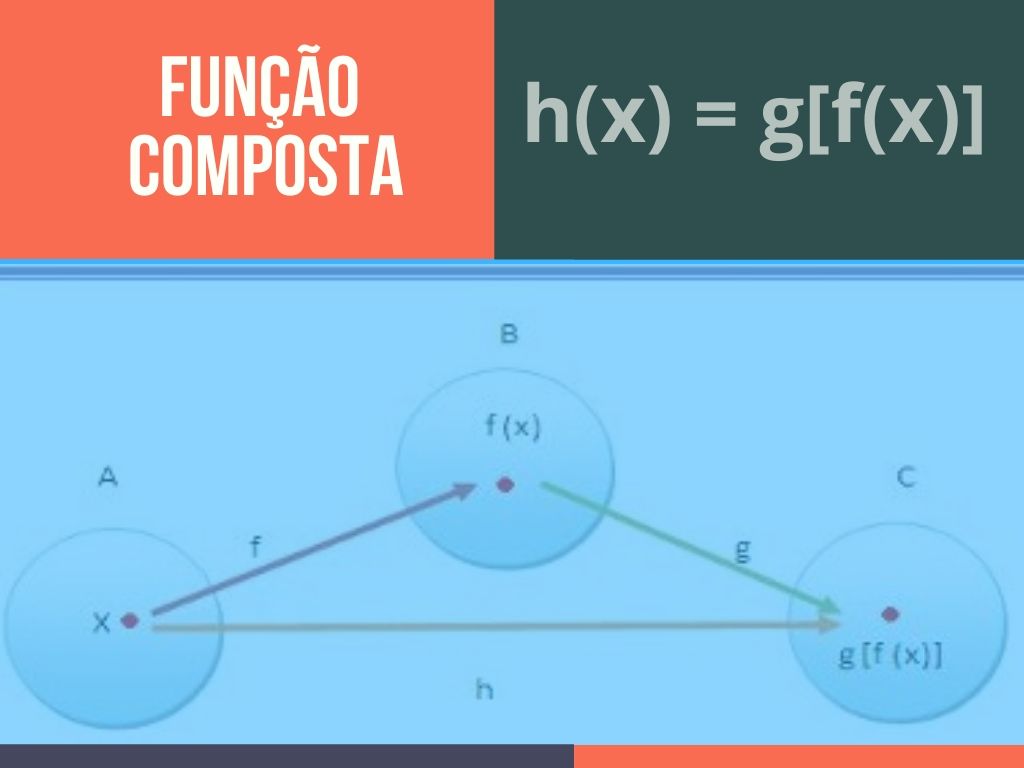
Definição: Considerando três conjuntos distintos A, B e C. Entre eles existem as seguintes funções: f: A→B e g: B→C. Irá existir outra função h: A→ C, assim a função h(x) = g(f(x)) é chamada função composta. Essa função composta também poderá ser indicada por g o f (lê – se: g composta com f). Veja o esquema a seguir:

Obs.: Atente para o fato de que fog ≠ gof, ou seja, a operação “composição de funções” não é comutativa.

Para determinar a função composta f[g(x)] basta substituir a variável independente de f pela função g e efetuar os cálculos.

O domínio de g deve ser a imagem de f e o domínio de f[g(x)] deve ser a imagem de g.

Exemplo: Dadas as funções f(x) = 2x + 3 e g(x) = 5x, Determine gof(x) e fog(x).
Teremos: gof(x) = g[f(x)] = g(2x + 3) = 5(2x + 3) = 10x + 15
fog(x) = f[g(x)] = f(5x) = 2(5x) + 3 = 10x + 3. Observe que fog ≠ gof .

Exemplo: Dados três conjuntos A = {-2, -1, 0, 3}, B = {-3,-2,-1,2} e C = {9,4,1,4}. Entre eles existem as seguintes funções: f: A->B definida por f(x) = x – 1 e g: B->C definida por g(x) = x². Para cada elemento de A existe um elemento em B tal que f(x) = x – 1 e para cada elemento de B existe um elemento de C tal que g(x) = x². Assim, pode-se concluir que existe uma função h: A->C definida por h(x) = g(f(x)), i.e, h(x) = x² – 1.

Exercícios resolvidos

1 - Sendo f e g duas funções tais que: f(x) = ax + b e g(x) = cx + d . Podemos afirmar que a igualdade gof(x) = fog(x) ocorrerá se e somente se:
a) b(1 - c) = d(1 - a)

b) a(1 - b) = d(1 - c)

c) ab = cd

d) ad = bc

e) a = bc

Solução: fog(x) = f[g(x)] = f(cx + d) = a(cx + d) + b => fog(x) = acx + ad + b
gof(x) = g[f(x)] = g(ax + b) = c(ax + b) + d => gof(x) = cax + cb + d

Como o problema exige que gof = fog, fica: acx + ad + b = cax + cb + d.

Simplificando, vem: ad + b = cb + d
ad - d = cb - b => d(a - 1) = b(c - 1), que é equivalente a d(a - 1) = b(c – 1),

2 - Dada a função f(x) = x² + 1 e g(x) = 3x – 4, calcule f(g(3));

Solução: Podemos proceder de duas maneiras: compor as funções depois achar o valor de f(g(3)) ou calcular g(3) depois substituir o valor encontrado em f.

(i) f(g(x)) = (3x-4)² + 1 = 9x² – 24x + 16 + 1. Agora basta calcular f(g(3)). Logo f(g(3)) = 9.3² – 24.3 + 16 + 1 = 81 – 72 + 17 = 26.

(ii)g(3) = 3.3 - 4 = 5. Substituindo esse valor em f: f(5) = 5² +1 = 26.

3 - Sendo f e g duas funções tais que fog(x) = 2x + 1 e g(x) = 2 - x então f(x) é:
a) 2 - 2x b) 3 - 3x c) 2x – 5 *d) 5 - 2x e) uma função par.

Solução: Sendo fog(x) = 2x + 1, temos: f[g(x)] = 2x + 1
Substituindo g(x) pelo seu valor, fica: f(2 - x) = 2x + 1
Fazendo uma mudança de variável, podemos escrever 2 - x = u, sendo u a nova variável. Portanto, x = 2 - u. Substituindo, fica: f(u) = 2(2 - u) + 1 => f(u) = 5 - 2u
Portanto, f(x) = 5 - 2x.