Definição:
Uma função f:R->R chama-se afim quando existem dois números reais a e b tal que f(x) = ax + b.
Exemplos:
f(x) = 3x + 12 ( a = 3 ; b = 12 );
f(x) = -3x + 1 (a = -3; b = 1).
Valor de uma função Afim: O valor de uma função f(x) = ax + b, para x = x0 é dado por f(x0) = a(x0) + b.
Por exemplo, seja a função afim: f(x) = 3x + 4. Determinar: f(1) e f(-3).
Solução:
- f(1) = 3.(1) + 4. Logo, f(1) = 7;
- f(-3) = 3.(-3) + 4. Logo, f(-3) = 1;
Valor inicial: Numa função afim o número b = f(0) chama-se valor inicial da função f.
Ex.: O valor inicial da função f(x) = 3x – 5 é -5 pois, f(0) = 3.(0) – 5 = – 5.
Propriedades da função afim:
1) o gráfico de uma função do 1º grau é sempre uma reta .
|
|
|
2) na função f(x) = ax + b, se b = 0, f é dita função linear. Se a = ±1 e b = 0, f é dita função identidade. Se a = 0, f é dita função constante.
Nota: O termo AFIM foi introduzido por Leonhard Euler (pronuncia-se óiler) - matemático suíço - 1701/1783.
3) o gráfico intercepta o eixo dos x na raiz da equação f(x) = 0 e, portanto, no ponto de abcissa x = - b/a.
4) o gráfico intercepta o eixo dos y no ponto (0, b), onde b é chamado coeficiente linear .
5) o valor a é chamado coeficiente angular e dá a inclinação da reta .
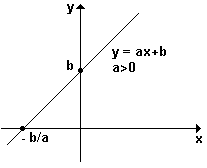
6) se a > 0, então f é crescente [x1 < x2 ⇒ f(x1) < f(x2)].
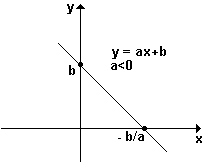
7) se a < 0, então f é decrescente [x1 < x2 ⇒ f(x1) > f(x2)].
8) quando a função é linear, ou seja, y = f(x) = ax, o gráfico é uma reta que sempre passa na origem e coincide com a 1º bissetriz (a > 0) ou com a 2º bissetriz (a < 0).
9) quando a função associa cada número real a ele mesmo é dita função identidade.
Calculo do coeficiente angular, inclinação, declividade ou taxa:
Se na função linear y = ax tirarmos o valor de a, obteremos: a = x/y.
Como os triângulos são semelhantes, Δx = x2 – x1 e Δy = y2 – y1, teremos para 2 pontos quaisquer A e B:





0 Comentários