A função y = f(x) é par, quando ∀x∈D(f), f(-x) = f(x), ou seja, para todo elemento do seu domínio, f(x) = f (-x). Portanto, numa função par, elementos simétricos possuem a mesma imagem. Uma conseqüência desse fato é que os gráficos cartesiano das funções pares, são curvas simétricas em relação ao eixo dos y ou eixo das ordenadas. Se (a,b) ∈ f ⇒ (-a,b) ∈ f.

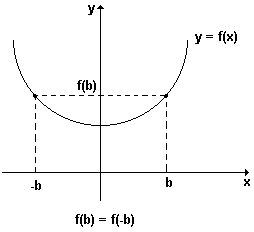
Exemplo: y = x⁴ + 1 é uma função par, pois f(x) = f(-x), para todo x. Pois, f(2) = 2⁴ + 1 = 17 e f(- 2) = (-2)⁴ + 1 = 17

Função ímpar: A função y = f(x) é ímpar, quando ∀x∈D(f), f(-x) = - f(x), ou seja, para todo elemento do seu domínio, f(-x) = - f(x). Portanto, numa função ímpar, elementos simétricos possuem imagens simétricas. Uma conseqüência desse fato é que os gráficos cartesianos das funções ímpares, são curvas simétricas em relação ao ponto (0,0), origem do sistema de eixos cartesianos. Se (a,b)∈f ⇒ (-a,-b)∈f.

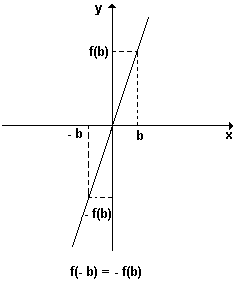
Exemplo: y = x³ é uma função ímpar pois para todo x, teremos f(- x) = - f(x).

Por exemplo, f( - 2) = (- 2)³ = - 8 e - f( x) = - ( 2³ ) = - 8.

Função sem paridade: Se uma função y = f(x) não é par nem ímpar, dizemos que ela não possui paridade. O gráfico, abaixo, representa uma função que não possui paridade, pois a curva não é simétrica em relação ao eixo dos y e, não é simétrica em relação à origem.

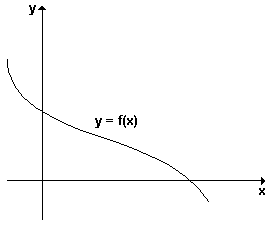
Exercícios Resolvidos

Para a resolução dos exercícios abaixo procederemos da seguinte forma: Primeiro verificaremos se a função é par depois se ela é impar e por fim se ela não tem paridade.

1 – Determine a paridade das funções abaixo:

a) f(x) = 2x + 3

Solução: f(-1) = 2.(-1) + 3 = 1; f(1) = 2.1 + 3 = 5 e –f(1) = -5. Como f(x) ≠ f(-x) e f(-x) ≠ -f(x) então a função não é par nem ímpar.

b) g(x) = x²

Solução: f(-1) = (-1)² = 1; f(1) = 1² = 1. Como f(x) = f(-x) então a função é par.

c) h(x) = e^x

Solução: f(-1) = e^(-1) = e^-1; f(1) = e¹ = e, e –f(1) = -e. Como f(x) ≠ f(-x) e f(-x) ≠ -f(x) então a função não é par nem ímpar.

d) f(x) = lnx

Solução: f(e) = ln e = 1; f(-e) = ln (-e) (não está definido, pois, ln x só está definido para x > 0); e –f(e) = -1. Como f(x) ≠ f(-x) e f(-x) ≠ -f(x) então a função não é par nem ímpar.

e) f(x) = sen(x)

Solução: f(-30°) = sen(-30°) = sen(330°) = -1/2; f(30°) = sen(30°) = 1/2 e –f(30°) = -1/2. Como f(-x) = -f(x) então a função é ímpar.

f) f(x) = cos(x)

Solução: f(-60°) = cos(-60°) = cos(300°) = 1/2; f(60°) = cos(60°) = 1/2. Como f(x) = f(-x) então a função é par.

Exercícios propostos

1 - Decida sobre a paridade das funções abaixo, se necessário esboce o gráfico:

a) f(x) = ln x²

b) f(x) = 1 + sen x

c) f(x) = 2 + cos x

d) f(x) = x³ + 1

e) f(x) = ln|x|