Estudar o sinal da função f(x) = ax + b é estabelecer para que valores de x teremos f(x) = 0, f(x) > 0, f(x) < 0.

f(x) = ax + b
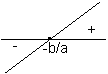
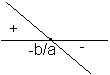
1º Caso (a > 0)	2º Caso (a < 0)
x < -b/a => f(x) < 0	x < -b/a => f(x) > 0
x = -b/a => f(x) = 0	x = -b/a => f(x) = 0
x > -b/a => f(x) > 0	x > -b/a => f(x) > 0

Obs: À direita da raiz o sinal é o mesmo de a e esquerda da raiz o sinal é oposto ao de a.

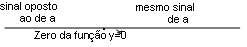
1º Caso: a > 0. Ex: f(x) = 2x – 6 é nula para 2x – 6 = 0 ⇒ x = 3.

 

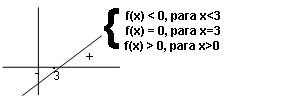
2º Caso: a < 0. Ex: f(x) = -2x + 6 é nula para -2x + 6 = 0 ⇒ x = 3.

 

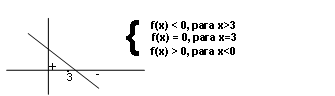
Representação gráfica da desigualdade.

 

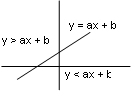
y < ax + b ⇒ regiao inferior                            

y = ax + b ⇒ pontos da reta

y > ax + b ⇒ região superior