Áreas e volumes
75 – (PETROBRÁS BIOCOMBUSTÍVEL 2010)
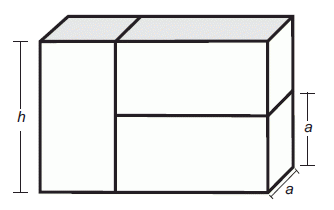
No modelo acima, estão representadas três caixas iguais (paralelepípedos reto-retângulos), de dimensões a, a e h. Se o conjunto ocupa 162 cm3, qual é, em cm2, a área total de cada caixa?
(A) 54
(B) 72
(C) 90
(D) 108
(E) 144
Resposta:
Na observação percebe-se que h = 2a
Volume:
a.2a.3a = 162
6a3 = 162
a3 = 27
a = 3
Area total da caixa:
a = 3
h = 6
AT = 2(3?3 + 3?6 + 3?6) = 90
Gabarito: C
76 – (PETROBRÁS DIST 2009) Placas retangulares de 20 cm de comprimento, 10 cm de largura e espessura desprezível serão acondicionadas em caixas quadradas, de 30 cm de lado, cuja espessura interna é igual à das placas.
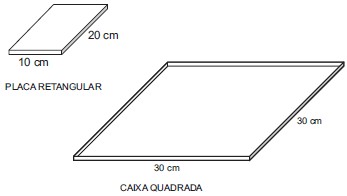
Dispondo-se de 4 dessas caixas, é possível acondicionar, no máximo, uma quantidade de placas igual a
(A) 15
(B) 16
(C) 17
(D) 18
(E) 20
Resposta:
Em cada caixa é possível inserir 4 placas.
Como são 4 caixas: 4.4 = 16.
Gabarito: B
65 – (PETROBRÁS DIST 2009) Uma folha de papel retangular, com 30 cm de comprimento e 21 cm de largura, será cortada em quatro partes iguais. Qual será, em cm2, a área de cada parte?
(A) 157,5
(B) 212,5
(C) 310,0
(D) 415,5
(E) 630,0
Resposta:
A área da folha de papel é: 630.
Daí, cada parte tem área: 630/4 = 157,5.
Gabarito: A
66 – (PETROBRÁS DIST 2009) Uma jarra cilíndrica de 6 cm de raio e 20 cm de altura está completamente cheia de suco. Com essa quantidade de suco, quantos copos de 300 ml podem-se encher?
(A) 5
(B) 6
(C) 7
(D) 8
(E) 9
Resposta:
Volume da jarra: ABase: h = π.62.20 = 720π = 720.3,14 = 2260,8cm3 = 2260,8ml
Basta agora dividir este volume por 300: 2260,8/300 = 7,536.
Dá para encher 7 caixas.
Gabarito: C
67 – (PETROBRÁS DIST 2010) Os tablets são aparelhos eletrônicos portáteis, maiores que um celular e menores que um netbook, ideais para a leitura de livros e jornais. Um dos primeiros tablets lançados no mercado americano tem a forma aproximada de um paralelepípedo reto-retângulo de 26,4 cm de comprimento, 18,3 cm de largura e 1 cm de espessura. Qual é, em cm3, o volume aproximado desse aparelho?
(A) 274,20
(B) 483,12
(C) 795,16
(D) 1.248,24
(E) 1.932,48
Resposta:
Volume: 26,4.18,3.1 = 483,12
Gabarito: B
68 – (PETROBRÁS DIST 2010) As cédulas de real estão sendo modernizadas. Elas continuarão a ser retangulares, mas, dependendo do valor, o tamanho será diferente. A menor delas será a de 2 reais, que medirá 12,1 cm por 6,5 cm. A maior será a de 100 reais, com 15,6 cm de comprimento e 7 cm de largura. Qual será, em cm2, a diferença entre as áreas dessas duas notas?
(A) 15,35
(B) 24,75
(C) 30,55
(D) 31,45
(E) 38,25
Resposta:
Área da de 2 reais: 12,1.6,5 = 78,65 cm2
Área da de 100 reais: 15,6.7 = 109,2 cm2
Diferença: 109,2 - 78,65 = 30,55
Gabarito: C
69 – (PETROBRÁS 2008) Um terreno retangular de 1.000 m2 é tal que seu comprimento mede 15 m a mais do que sua largura. O perímetro desse terreno, em metros, é
(A) 40
(B) 65
(C) 130
(D) 220
(E) 400
Resposta:
Largura: x
comprimento: x + 15
Daí, x ?(x + 15) = 1000
x = 25
Largura: 40
Comprimento: 40
Perímetro: 25 + 25 + 40 + 40 = 130.
Gabarito: C
62 – (PETROBRÁS 2008) Um aquário de forma cúbica estava parcialmente cheio de água quando uma pedra de 750 cm3 de volume foi colocada em seu interior. Assim, o nível da água subiu 0,3 cm.
Qual é, em cm, a medida da aresta desse aquário?
(A) 30
(B) 40
(C) 50
(D) 60
(E) 70
Resposta:
Volume antes da pedra: Vantes = a2.x
Volume depois da pedra: Vdepois = a2 . (x + 0,3) = a2.x + 0,3.a2
Dái, volume da pedra: 0,3.a2 => 0,3?a2 = 750 => a2 = 2500 => a = 50
Gabarito: C



0 Comentários